無機化学やX線解析実験などの分析化学においてでてくるブラべ格子。
このブラべ格子を理解するには、結晶の3次元的な空間を想像しなければいけません。
空間図形が苦手だった人にとっては苦痛だと思います。
今回は、それを言葉で整理することで、ブラべー格子を理解していきましょう。
ブラべー格子とはなにか。
まず結論からおさえておきましょう。
ブラべー格子とは、”単位格子の分類”です。
これがまず大前提になります。とても大雑把な説明ですので、これから詳しく説明していきます。
ブラベー格子を理解する下準備
ブラベー格子を理解するために、まずそもそも
・単位格子
について理解しているでしょうか?
もしも理解できていなかったらまずは復習からはじめましょう。
ブラベー格子を理解するには、
「単位格子の”形”が3つの長さ(a,b,c)と3つの角度(α,β,γ)によって決められる」
ことを思い出しておかなければなりません。
7の結晶系と14のブラベー格子
それではブラベー格子の話にもどります。
先ほど、ブラべー格子とは、”単位格子の分類”です。
という風に言いました。
しかし、同じように単位格子の分類をしているもう一つの用語を覚えておきましょう。
それは、結晶系です。
結晶系もブラベー格子と同じように単位格子の分類をしているわけですが、
結論から言うと、結晶系をさらに細かく分けたのがブラベー格子です。
結晶系は7種類。そして、この7種類を細かく分けたものがブラベー格子です。
そしてそのブラベー格子は14種類です。
・結晶形は7種類。ブラベー格子は14種類
7つの結晶系
まず、7つの結晶系について考えましょう。
先ほど、単位格子の”形”が3つの長さと3つの角度によって決まることも復習しました。
このとき、その長さと角度の関係から単位格子を分類したものが結晶形です。
次の表は結晶系をまとめたものです。
| 名称 | 辺の長さの条件 | 角度の条件 |
| 三斜晶系 | $$ a \neq b \neq c $$ |
$$ \alpha \neq \beta \neq \gamma \neq 90^{\circ} $$ |
| 単斜晶系 | $$ a \neq b \neq c $$ |
$$ \alpha=\gamma=90^{\circ}, \quad \beta \neq 90^{\circ} $$ |
| 斜方晶系 | $$ a \neq b \neq c $$ |
$$ \alpha=\beta=\gamma=90^{\circ} $$ |
| 正方晶系 | $$a=b \neq c$$ | $$ \alpha=\beta=\gamma=90^{\circ} $$ |
| 三方晶系 | $$a=b=c$$ | $$ \alpha=\beta=\gamma \neq 90^{\circ} $$ |
| 六方晶系 | $$a=b \neq c$$ | $$ \alpha=\beta=90^{\circ}, \quad \gamma=120^{\circ} $$ |
| 立方晶系 | $$a=b=c$$ | $$ \alpha=\beta=\gamma=90^{\circ} $$ |
ブラベー格子の分類
さきほど確認した結晶系からブラベー格子はどのように分けられるのでしょうか。
結論から言うと、単位格子を構成する原子や分子の配置の仕方でブラベー格子は区別されます。
配置の仕方とは、単純、体心、面心、底心の4種類です。
もし、この配置の意味がわからない場合は復習が必要です。
つまり、7つの結晶形それぞれに4種類の粒子の配置の仕方があるので、7×4通り。つまり28通りの単位格子が考えられます。
でも、ブラベー格子は14種類…
そう、この28通りのなかに結果として同じ配置になる単位格子が含まれているのです。これを一つ一つ除外していくと、
ブラベー格子は14通りだけ残ります。
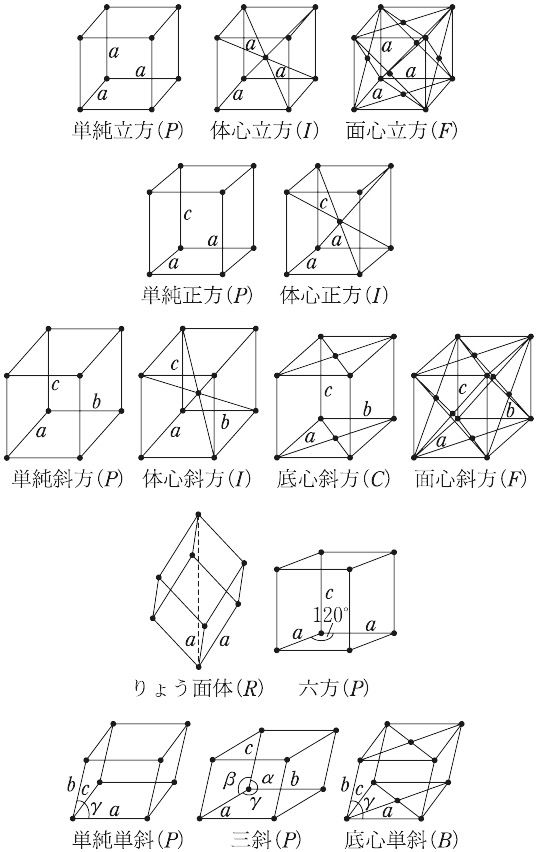
↑14種類のブラべ格子 森北出版「化学辞典(第2版)」より引用
参考書籍
この内容を理解するには、次の参考書がおすすめです。
また、無機化学全体を眺めたいなら
がおすすめです。
無機化学の教科書 シュライバー・アトキンス無機化学 → シュライバー・アトキンス無機化学 (上) はこちら シュライバー・アトキンス無機化学は、東京化学同人から出版されている無機化学の教科書です。 多くの大学で使わ[…]
X線による結晶構造の決定について学びたいなら、
を読んでみるといいでしょう。




