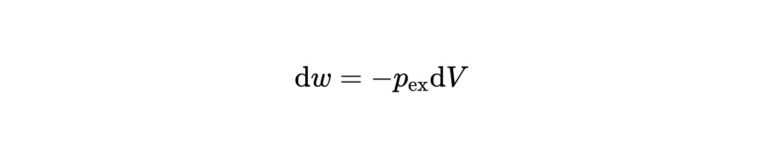膨張の仕事を求める

膨張の仕事

まず、膨張の仕事が何かということについて知っておきましょう

膨張の仕事とは、気体が大気を押しのけて膨張する時、あるいは圧縮される時に気体によってなされる仕事です。

外からの圧力を\(p_{\mathrm{ex}} \)とすると、膨張の仕事は次のように表されます。

$$\mathrm{d} w=-p_{\mathrm{ex}} \mathrm{d} V$$

さらに体積がViからVfまで変化する時の仕事を求めるためには、この式を積分します。

$$w=-\int_{V_{i}}^{V_{f}} p_{\mathrm{ex}} \mathrm{d} V$$

このとき符号に注意する必要があります。\(w\)は、系の気体が”なされた”仕事であるため、体積の増加が正であるとき(膨張する時)、仕事は負の値をとります。逆に、体積が減少する時(圧縮される時)、仕事は正の値になります。

一定圧力による膨張

基本的にどんな膨張の仕事も

$$w=-\int_{V_{i}}^{V_{f}} p_{\mathrm{ex}} \mathrm{d} V$$

を使って求めることになりますが、

このとき、外からの圧力が一定のとき、つまり\(p_{\mathrm{ex}} \)が一定のとき、\(p_{\mathrm{ex}}=0 \)であるので、

\(p_{\mathrm{ex}} \)を積分の外にだすことができます。よって

$$w=-p_{\mathrm{ex}} \int_{V_{1}}^{V_{\mathrm{f}}} \mathrm{d} V$$

と表され、積分の部分を計算すると、

$$w=-p_{\mathrm{ex}}\left(V_{\mathrm{f}}-V_{\mathrm{i}}\right) $$

これを体積変化\(\Delta V=V_{\mathrm{f}}-V_{\mathrm{i}}\)を使って表すと

$$w=-p_{\mathrm{ex}} \Delta V$$

という式にまとめられます。

自由膨張\((p_{\mathrm{ex}} =0)\)による仕事

自由膨張とは、外圧が0とみなせる状態でおこる変化です。

このときも

$$w=-\int_{V_{i}}^{V_{f}} p_{\mathrm{ex}} \mathrm{d} V$$

を用いて仕事を考えてみます。

外圧が0であるので、\(p_{\mathrm{ex}} =0\)である。

すぐに、\(w=0\)であることがわかります。

可逆膨張

可逆反応とは平衡との関わりが強く、平衡にある系は可逆反応を行なっていると言えます。

外圧と容器内の気体の圧力が等しいとき、両者は力学的平衡の関係にあるため、可逆膨張を行います。

つまり、可逆膨張の仕事は、

$$w=-\int_{V_{i}}^{V_{f}} p_{\mathrm{ex}} \mathrm{d} V$$

において、\(p_{\mathrm{ex}} = p\)とすることで、

$$w=-\int_{V_{i}}^{V_{f}} pdV$$

という風に外部の圧力の代わりに内部の圧力を用いて仕事を表現することができます。

等温可逆膨張

可逆膨張の中でも、完全気体で等温の場合を考えます。

先ほど求めた、

$$w=-\int_{V_{i}}^{V_{f}} pdV$$

の式に、\(p = nRT/V\)であることを使い、

$$w=-nRT\int_{V_{\mathrm{i}}}^{V_{\mathrm{f}}} \frac{\mathrm{d} V}{V}$$

と表すことができます。

結果として、等温可逆膨張の仕事は次のようになります。

$$w=-n R T \ln \frac{V_{\mathrm{f}}}{V_{\mathrm{i}}}$$

まとめ

膨張の仕事は、次のような式で表されます