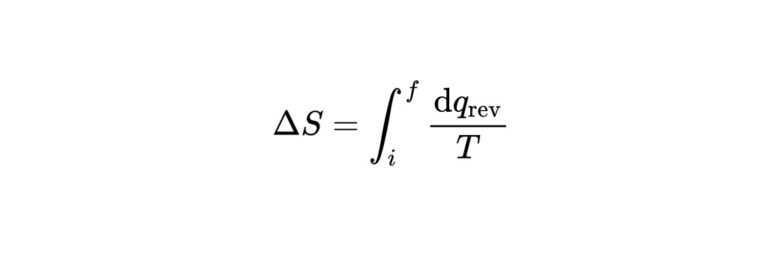エントロピーとは散らばり具合を示す指標であると、よく言われます。
しかし、それだけでは納得できない人も多いでしょう。
ここでは、定義からエントロピーが何かをはっきりさせてみましょう。
ざっくりまとめると…
エントロピーの2つの定義
・熱力学的な方法 … エネルギーの散らばり具合を熱として運ばれるエネルギーとして見て、ある過程で起きたエントロピーの変化を定義するもの。
・分子論的な方法 … 散らばり具合をエネルギー準位の分布と関連づけることで定義されたもの。統計的エントロピーとも言われる。
つまり、散らばり具合を熱という無秩序な運動と関連づけた定義の仕方と、エネルギー準位の分布という統計的にみた定義の仕方があるということです。
詳しく見てみると…
エントロピーの熱学的な定義
エントロピー変化の熱学的な定義はこちらです。
$$\mathrm{d} S=\frac{\mathrm{d} q_{\mathrm{rev}}}{T}$$
ある系の二つの状態でのエントロピーの差を求めるには、まずその二つの可逆な経路を見つけ、そこで熱として供給されたエネルギーをそのときの温度で割って積分すれば求められる。つまり、以下の積分式で表すことができます。
$$\Delta S=\int_{i}^{f} \frac{\mathrm{d} q_{\mathrm{rev}}}{T}$$
エントロピーの統計的な定義
原子や分子はある絶対温度Tにおいて熱運動による特定のエネルギーの値を持ちます。
このような考えを発見したボルツマンはさらに、このいわゆるエネルギー準位をエントロピーと関連づけました。
結論から言うと、次のようになります。
$$S=k \ln \mathcal{W}$$
\(k\):ボルツマン定数 =1.38064852 × 10-23 m2 kg s-2 K-1
\(W\): 微視的状態の取りうる数
ここでの、\(W\)は、いわゆるmicrostate(微視的状態の数)と言われ、全エネルギーが変わらないように分子や原子を配置するときのとりうる配置の数のことです。
これによって、散らばり具合や散逸さと言われた抽象的なエントロピーの観念を、微視的状態の取りうる数という定量的に概念化することができます。
ボルツマンのエントロピーの式において、\(W=1\)、つまりとりうる状態の数が一つしかない時、\(S=0\)となります。
\(W>1\)となるにつれて(取りうる状態の数が増えるにつれて)、エントロピーは増大し、\(S>0\)へと変化していきます。
熱力学的定義と統計的定義の関連性
統計的なエントロピーの定義を知った後で、熱力学定義の式を見てみるとその意味がはっきりとしてきます。
$$\Delta S=\int_{i}^{f} \frac{\mathrm{d} q_{\mathrm{rev}}}{T}$$
この熱力学的において分母の\(T\)に着目してください。
系の温度が高いとき、エネルギー準位の考え方より系が取りうる状態は温度が低い時よりも多く、
少し熱を与えたくらいでは、系のとりうる状態は大きく増加することはありません。
しかし、温度が低い時なら少しの熱で系のとりうる状態は大きく増えることになります。
つまり、この温度Tが分母にあることで、エネルギー準位の熱学的な定義と統計学的な定義の関わりあいをみることができます。
まとめ
・エントロピーの定義は2種類
・熱力学な定義は、散らばり具合を熱の無秩序な運動と結びつけ数式で表したもの
$$\mathrm{d} S=\frac{\mathrm{d} q_{\mathrm{rev}}}{T}$$
・統計学的な定義は、散らばり具合をエネルギー準位と結びつけて表したもの
$$S=k \ln \mathcal{W}$$