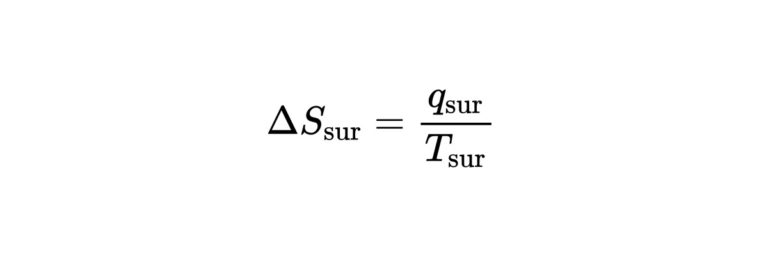外界のエントロピー
問題を解くうえで系のエントロピーと外界のエントロピーをきちんと区別する必要があります。
系のエントロピーは、
$$\mathrm{d} S=\frac{\mathrm{d} q_{\mathrm{rev}}}{T}$$
と表されますが、
外界のエントロピーも同様に表すことができます。
外界は、系と比べて、体積が大きく体積一定とみてよく、熱として与えられたエネルギーは、内部エネルギーの変化とみてよい。
内部エネルギーは状態関数であるので、その変化量は可逆・不可逆問わない。
つまり、外界のエントロピー変化は、可逆でなくても、
$$\mathrm{d} S=\frac{\mathrm{d} q_{\mathrm{rev}}}{T}$$
が成り立つということを示す。
このことは、可逆を表す下付き文字のrevをつけなくてもよいので、
$$\Delta S_{\mathrm{sur}}=\frac{q_{\mathrm{sur}}}{T_{\mathrm{sur}}}$$
が成立します。
補足 \(\Delta S\)と\(\mathrm{d} S\)は何が違うか
意外とよくわからないのが、\(\Delta S\)と\(\mathrm{d} S\)の違いです。
微小記号の\(\mathrm{d}\)は、系の変化が無限小で可逆的なときに用いられます。
一方、\(\Delta\)は、可逆・不可逆は関係なく変化量を表します。
上の式で\(\Delta S\)が用いられているのは、可逆不可逆が関係ないことを示唆しています。
断熱変化時の外界のエントロピー変化
$$\Delta S_{\mathrm{sur}}=\frac{q_{\mathrm{sur}}}{T_{\mathrm{sur}}}$$
この式から一目瞭然ですが、断熱変化のときのエントロピーの変化は、当然0になります。
$$\Delta S_{\mathrm{sur}}=0$$
これは、先ほど確認したように、可逆・不可逆反応に関わらず成立します。
外界が一定圧力のとき
外界が一定圧力であるとみなせるときは、\(\mathrm{d} q_{\mathrm{sur}}\)が\(\mathrm{d} H_{\mathrm{sur}}\)に等しいとみなせるため、運ばれた熱の代わりにエンタルピーの変化\(\mathrm{d} H_{\mathrm{sur}}\)を用いて良いことになります。
まとめ
・外界のエントロピー変化も、系のエントロピー変化同様に、以下の式が成り立つ。
$$\mathrm{d} S=\frac{\mathrm{d} q_{\mathrm{rev}}}{T}$$
・外界のエントロピー変化の場合は、可逆・不可逆関係なく成り立つため、さらに次のようにかける。
$$\Delta S_{\mathrm{sur}}=\frac{q_{\mathrm{sur}}}{T_{\mathrm{sur}}}$$
・断熱変化の場合は、いかなる場合も外界のエンタルピー変化は0になる。