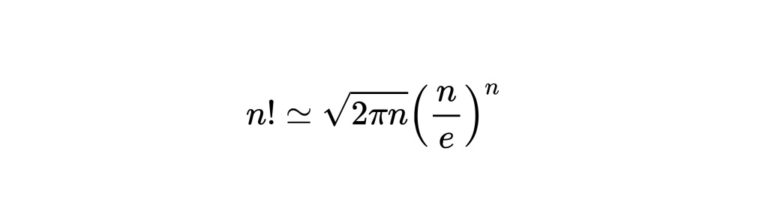統計の分野でよく使うスターリングの公式について説明します。
物理化学などで統計の知識は必要です。そのなかでも自然対数に関する近似式としてスターリングの公式を覚えておくと便利でしょう。
スターリングの公式
結論から言うと、スターリングの公式は次のように表されます。
$$
n ! \simeq \sqrt{2 \pi n}\left(\frac{n}{e}\right)^{n}
$$
これはよく使われる形ですが、場合によってはより厳しく評価したり、ゆるく評価したりすることもできます。
これらは、次のようにまとめられます。
n ! \simeq \sqrt{2 \pi n}\left(\frac{n}{e}\right)^{n}
$$より厳しい形
$$
n ! \simeq \sqrt{2 \pi n}\left(\frac{n}{e}\right)^{n}\left(1+\frac{1}{12 n}\right)
$$
よりゆるい形
$$
n ! \simeq\left(\frac{n}{e}\right)^{n}
$$
スターリングの公式の証明
今回は厳密な証明でなく、一番ゆるい式をかなりアバウトな形で求めてみます。
目標
$$
n ! \simeq\left(\frac{n}{e}\right)^{n}
$$
証明
n!の対数を取ると、Σを使って次のように表せます。
$$
\ln (n !)=\ln [n(n-1) \cdots 3・2・1]=\sum_{k=1}^{n} \ln k
$$
一般にnが限りなく大きく、\(\Delta x=\frac{\mathbf{b}-\mathbf{a}}{\mathbf{n}}\)の時に次のように近似できます(区分求積法による)。
$$
\lim _{n \rightarrow \infty} \sum_{k=1}^{n} f\left(x_{k}\right) \Delta x=\int_{a}^{b} f(x) d x
$$
これを用いると、次のように大雑把に表してもいいでしょう。
$$
\sum_{k=1}^{n} \ln k=\int_{1}^{n}(\ln x) d x
$$
右側の積分は、対数の基本の積分なので部分積分を用いて\(n\ln n-n\)であることがわかります。
これを用いると、結果的に
$$
\ln n! \simeq n \ln n-n
$$
となります。
あとは、対数を外すことによって目標となるスターリングの公式が得られます。
$$
n ! \simeq\left(\frac{n}{e}\right)^{n}
$$