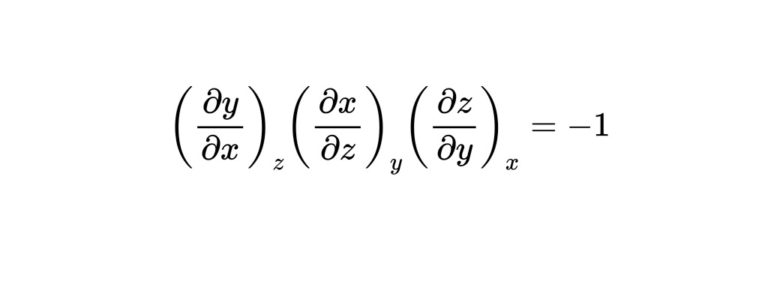大学に入って、数学、物理、化学など多くの分野で出現し直感的に掴みづらいオイラーの連鎖式。
今回はその導出をみてみることで、オイラーの連鎖式を深く学習して感覚を掴んでいきましょう。
オイラーの連鎖式
結論から言うと、オイラーの連鎖式は次のように表されます。
$$\left(\frac{\partial y}{\partial x}\right)_{z}\left(\frac{\partial x}{\partial z}\right)_{y}\left(\frac{\partial z}{\partial y}\right)_{x}=-1$$
見かけは綺麗な形ですが、右辺の−1がくせものです。
オイラーの連鎖式の導出
この導出について理解するためには全微分について理解しておかなければなりません。
x,y,zは互いに依存しており、一つが決まれば、他二つが決まるとする。
そんなとき、x,yの全微分はそれぞれ次のように表されます。
$$
d x=\frac{\partial x}{\partial y} d y+\frac{\partial x}{\partial z} d z
$$
$$d y=\frac{\partial y}{\partial z} d z+\frac{\partial y}{\partial x} d x$$
上の式の\(d y\)に下式の\(d y\)を代入し、計算すると次のようになります。
$$
\begin{aligned}
d x &=\frac{\partial x}{\partial y}\left(\frac{\partial y}{\partial z} d z+\frac{\partial y}{\partial x} d x\right)+\frac{\partial x}{\partial z} d z \\
&=\frac{\partial x}{\partial y} \frac{\partial y}{\partial x} d x+\left(\frac{\partial x}{\partial y} \frac{\partial y}{\partial z}+\frac{\partial x}{\partial z}\right) d z \\
&=d x+\left(\frac{\partial x}{\partial y} \frac{\partial y}{\partial z}+\frac{\partial x}{\partial z}\right) d z
\end{aligned}
$$
最後の式から左辺、右辺共通する\(d x\)を消すと、次の式が得られます。
$$
\left(\frac{\partial x}{\partial y} \frac{\partial y}{\partial z}+\frac{\partial x}{\partial z}\right) d z=0
$$
任意のzでこれが成り立たつためには、係数部分が0でなければなりません。すると上の式から
$$
\frac{\partial x}{\partial y} \frac{\partial y}{\partial z}+\frac{\partial x}{\partial z}=0
$$
が得られます。第2項を移項すると、次のようになり、
$$
\frac{\partial x}{\partial y} \frac{\partial y}{\partial z}=-\frac{\partial x}{\partial z}
$$
つづいて逆関数の微分の関係\(\left(\frac{\partial y}{\partial x}\right)_{z}=\frac{1}{(\partial x / \partial y)_{z}}\)を使うと
結論となるオイラーの連鎖式が求められます。
$$\left(\frac{\partial y}{\partial x}\right)_{z}\left(\frac{\partial x}{\partial z}\right)_{y}\left(\frac{\partial z}{\partial y}\right)_{x}=-1$$