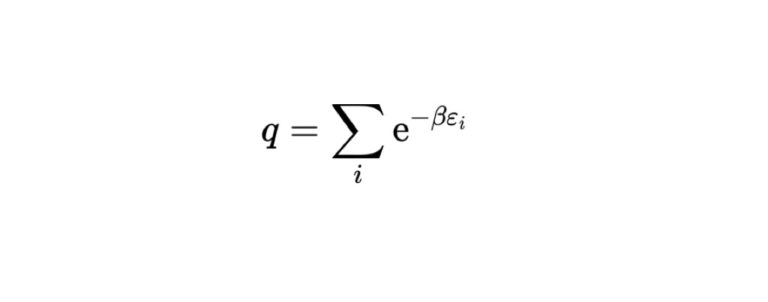今回は、統計熱力学などで用いられる分配関数について説明します。
分配関数の定義は、教科書によって異なることもあります。
今回は「アトキンス物理化学(下)第10版」に書かれている式を参考に分配関数を説明します。
分配関数とはなにか?
結論から言うと分配関数は
$$
q=\sum_{i} \mathrm{e}^{-\beta \varepsilon_{i}}
$$
$$
(\beta=\frac{1}{k T})
$$
\(k\):ボルツマン定数
という風に表されます。
では、この式は何を意味しているのでしょうか。
この意味を知るにはボルツマン分布について知っておかなければいけません。
$$
\frac{N_{i}}{N}=\frac{\mathrm{e}^{-\beta \varepsilon_{i}}}{\sum_{i} \mathrm{e}^{-\beta \varepsilon_{i}}}
$$
分配関数の意味
さてボルツマン分布の分母が分配関数であることがわかりました。
このことから言える分子関数の意味はなんでしょう。
アトキンス物理化学(下)第10版には、
“分子関数”の名は、全分子数がすべての取りうる状態にどのように分布しているか,分配されているか,の目安をqが与えてくれることを意味している.
とあります。
数学などで扱う確率、例えば、サイコロでの確率では分母が6(1〜6の6通り)です。
しかし、ボルツマン分布の分母にある分配関数は定数ではありません。
なぜなら、分配関数の中にはβというパラメーターがあり、またそのなかには絶対温度が変数として含まれます。
つまり、温度が変わればあるエネルギー準位を取りうる分子数は変わります。
さらには、どの程度の範囲に分子が分布するかも変わります。
アトキンス物理化学(下)第10版には逆に、次のように書かれています。
熱平衡にある系が最もとりやすい配置をとるとき,その各状態の占有数を決める唯一のパラメーターが温度である.
つまり、分子全体を見渡した時に、どの程度の温度範囲に分布が広がっているかの目安となります。
確率における母集団と区別して考えましょう。
参考:アトキンス物理化学(下)
分子分配関数を理解するのに役だつ参考書・教科書としてアトキンス物理化学(下)第10版をお勧めします。
アトキンス物理化学はなるべく計算せず、定性的に理解できるようになっています。
そのため複雑な計算式や数学が苦手という人でも理解しやすい内容になっています。