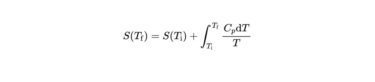熱力学第3法則とネルンストの熱定理

エントロピーが理論的になにかわかったとして、
実際のところ物質のエントロピーをどのように求めればいいか疑問に思う人も多いと思います。

ここでは、エントロピーの測定手段について解説します。ここでの鍵になるのは、熱力学第三法則です。

KEY …　熱力学第3法則 ネルンストの熱定理

エントロピーの2種類の測定

エントロピーの測定方法は大きく分けて2種類あります。

・T=0から温度をあげていき、必要となった熱量を調べる方法

・理論計算によってボルツマンによる統計エントロピーを求める方法

この記事では、上の「T=0から温度をあげていき、必要となった熱量を調べる方法」についてみていきます。

熱量測定によるエントロピーの測定

以前の記事で、温度変化によるエントロピーの変化を求める方法を学びました↓

この記事の中で、温度変化によるエントロピーの変化の式として

$$
S\left(T_{\mathrm{f}}\right)=S\left(T_{\mathrm{i}}\right)+\int_{T_{\mathrm{i}}}^{T_{\mathrm{f}}} \frac{C_{p} \mathrm{d} T}{T}
$$

を使えばよいことがわかりました。

熱量測定でエントロピーを測定していくときも、この式を用いてエントロピーの変化を測定していきます。

具体的には、最初の温度をT=0と設定してそこからだんだんと温度をあげていきます。

注意しなければいけないのは、途中で固体→液体→気体などど状態が変化するときは、温度変化によるエントロピーの変化に加えて、状態変化に伴う転移エントロピーを加えなければならないということです。

これを一般的に表すとこのように表せます。必要に応じて式の一部をとって使います。

\begin{eqnarray}
S_{\mathrm{m}}(T)=S_{\mathrm{m}}(0)&+&\int_{0}^{T_{\mathrm{f}}} \frac{C_{p, \mathrm{m}}(\mathrm{s}, T)}{T} \mathrm{d} T+\frac{\Delta_{\mathrm{fus}} H}{T_{\mathrm{f}}}\\
&+&\int_{T_{\mathrm{f}}}^{T_{\mathrm{b}}} \frac{C_{p, \mathrm{m}}(l, T)}{T} \mathrm{d} T+\frac{\Delta_{\mathrm{vap}} H}{T_{\mathrm{b}}}\\
&+&\int_{T_{\mathrm{b}}}^{T} \frac{C_{p, \mathrm{m}}(\mathrm{g}, T)}{T} \mathrm{d} T
\end{eqnarray}

ネルンストの熱定理と熱力学第3法則

ネルンストが取りまとめたネルンストの熱定理では、どんなに頑張っても固体を絶対零度まで下げることは不可能なことを意味します。

なぜなら、物体の温度を下げるためには、さらに低い温度のものを近接させなければいけません。ということは、絶対零度にするためには、絶対零度よりも低い温度のものを近接させなければいけませんが、そんな物体は存在しません。

また、この考えの言い換えとして、温度が絶対零度に近づくにつれて、エントロピー変化も0に近づいていくという事が言えます。

$$
\lim _{T \rightarrow 0} \Delta S=0
$$

また、エントロピー変化が0に近づくということは、極低温ではいかなる反応も起こりづらく、熱運動もないため、完全に秩序だった形をとることが予測されます。

プランクは、このネルンストの熱定理を発展させて完全結晶において、T=0においてエントロピー自体が0となることを導き出しました。

このことは、このように表されるでしょう。

$$
\lim _{T \rightarrow 0} S=0
$$

これを熱力学第三法則といいます。

上のネルンストの式と熱力学第三法則の違いをおさえておきましょう。

まとめ

・ネルンストの熱定理とは、T=0に近づくにつれてその近辺の温度で行ういかなる変化に伴うエントロピーの変化も0に近づくというもの。

・熱力学第三法則とは、ネルンストの定理から発展したもので、完全結晶の形をとるどんな物質もT=0のときのエントロピーは0とみなせるというもの。

・完全結晶とは、結晶のなかで不純物や格子欠陥が存在しないものです。