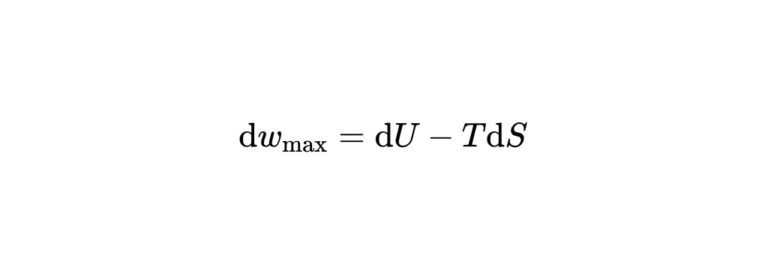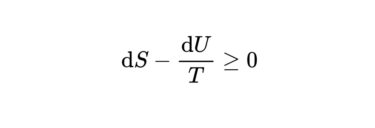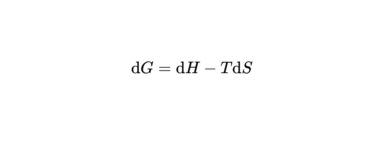以前の記事で等温かつ等積のとき、ヘルムホルツエネルギーが反応の自発性の判断に使えるという話をしました。
ヘルムホルツエネルギーとギブズエネルギーはよく似た式です。 その違いとそしてその意味について学習しましょう。 クラウジウスの不等式の利用 エントロピーは、反応がどのような方向に進むかの指標でした。 しかし、それを使うためには[…]
しかし、ヘルムホルツエネルギーにはもう一つ大切な意味が隠されています。
ヘルムホルツエネルギーと最大仕事
結論から言うと、ヘルムホルツエネルギーの変化は等温で引き起こせる最大の仕事に等しくなります。
そのためしばしばヘルムホルツエネルギーは仕事関数や最大仕事関数などと言われます。
これを式で表すと次のようになります。
$$
\mathrm{d} w_{\max }=\mathrm{d} A
$$
ヘルムホルツエネルギーの変化が最大仕事になる根拠
ヘルムホルツエネルギー変化と最大仕事の関係を示すには、クラウジウスの不等式と熱力学第一法則を用いる必要があります。
クラウジウスの不等式 \(\mathrm{d} S-\frac{\mathrm{d} q}{T} \geq 0\)を変形した形
$$
T \mathrm{d} S \geq \mathrm{d} q
$$
に対して、熱力学第一法則 \(\mathrm{d} U=\mathrm{d} q+\mathrm{d} w\)を\(\mathrm{d} q\)を消す形で用いると、
$$
\mathrm{d} U \leq T \mathrm{d} S+\mathrm{d} w
$$
という形になります。これを仕事が主役になるように変形すると、
$$
\mathrm{d} w \geq \mathrm{d} U-T \mathrm{d} S
$$
という風になります。
このとき、仕事が負に最大になるとき系がした仕事は最大になることから等号が成立したときが最大の仕事となります。
つまり、
$$
\mathrm{d} w_{\max }=\mathrm{d} U-T \mathrm{d} S
$$
となります。これはヘルムホルツエネルギーと等しくなります。