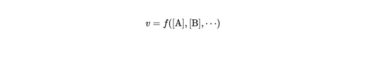統計学などにでてくる等確率の原理(当重率の原理)について説明します。
これはボルツマン分布などへと繋がる大事な概念です。
等確率の原理がなに?という人には必見です。
等確率の原理とは
等確率の原理とは簡単に言うと、
「同等のエネルギー状態を持つ状態はいずれも同じ程度に起こる可能性をもつ」
というものです。
ただし、これは平衡状態になっているときの巨視的な目線での話です。
微視的にみると、同じエネルギー状態でも無数の状態が存在します。
つまり、これは巨視的な目線からものを考える熱力学などの理論を支えるものになります。
もっと詳しく
ここまでは熱力学や統計学の教科書に載っている説明ですが、わかったようでわからないような感じがします。
もっと具体的にどういうことなのかを考えてみましょう。
たとえば…
例えば、気体の温度を測定したとします。このとき、気体といっても無数の分子が存在しています。
そして無数の分子は無数の状態をもちます(微視的な視点)。ということは、一つ一つの分子単位でみると温度はどれも違います。
では、先ほど我々が測った温度とは一体何なのでしょうか?
この温度はいわゆる巨視的な目線でみたときの温度で、それぞれの分子の平均と言っても差し支えないでしょう。
さらには、時間の変化によっても分子の温度は刻一刻と変わっていきます。
このような、分子や時間の変化を考えていては熱力学は扱えないため、平衡状態(巨視的な状態)において一つの限定された状態に限るという仮定をします。
これが等確率の原理です。
参考書
これまでの説明はとても大雑把なものです。
正確な意味を理解するには、さらに詳しい参考書や専門書を読む必要があるでしょう。
ここでは、初心者向け、上級者向けに等確率の原理を説明した参考書を紹介します。
初心者向けの参考書
この中で一番おすすめなのは最後のビジュアルアプローチ熱・統計力学です。
この参考書は代々木ゼミナールで物理を教えていた為近和彦さんが書いた本です。
普段高校生を教えているだけに高校から大学への架け橋となる本になっています。
熱力学や統計力学をカラーの図でわかりやすく説明しています。