【大学院試験対策】最確分布(ボルツマン分布)

化学系の大学院試験直前の対策として、大学院の試験に出題されうる大事な用語やキーワードの説明や導出をしています。

今回は物理化学、化学熱力学の分野の中から最確分布(ボルツマン分布)というテーマを扱っていきます。

最確分布(ボルツマン分布)

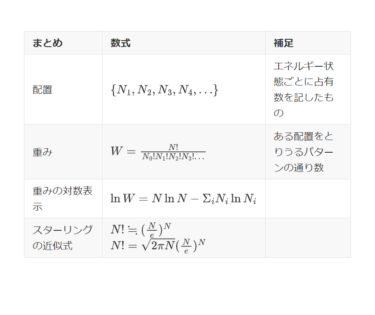
最確分布について学習する前に配置と重みについておさらいすると、

配置とは、それぞれのエネルギー準位に所属する分子数を表したもので、重みとはその配置が起こる通り数を示すものです。

全体の配置に対して、ある配置がきわめて大きな重みをもつ場合には、

ほとんど常にその配置が見いだされることになるので、系の性質はその配置が決めると言ってもいいでしょう。

このときのエネルギー準位に対する分子の配置を最確分布と言います。

より限定的な言い方をすると、これはボルツマン分布と呼ばれています。

最確分布ということは、最もその配置が起こりうる可能性が一番高いものになります。

そこで重みWが最大になるような配置を調べます。

最大になる配置を求めるので、必要条件として極値を探し出します。

そのような極値は、$dW=0$​あるいは、$d\ln W=0$​である点を探せばいいということになります。

制約条件

重みの最大な配置を探し出すときに条件があります。

条件と言っても常識的に考えられるようなものです。

その条件とは

・エネルギーに関する条件

・分子数に関する条件

となります。

エネルギーに関する条件

孤立系では全分子を合わせたエネルギーは一つに決まるので、全エネルギーをEとし、各エネルギー準位を$ε_i$と表すと、次のような制約があります。

$\sum\limits_{i} N_iε_i=E$​

分子数に関する条件

さらに、それぞれのエネルギー状態に入る分子数の合計は常に一定であるので、分子数に関する条件は次のように表されます。

$\sum\limits_{i}{} N_i=N$​

ボルツマン分布の導出

これら二つの条件は、エネルギー状態の占有数に微小量の変化があったときに、その変化の総和が0になるという表現で使います。つまり、次のようになります。

$\sum\limits_{i} ε_idN_i=0$

$\sum\limits_{i} dN_i=0$

また,

$d\ln W=\sum\limits_{i}{}(\frac{\partial \ln W}{\partial N_i})dN_i$​​

であり、$d\ln W=0$であるとして極大値を求めます。

そのときに用いる手法がラグランジュの未定乗数法です。

ラグランジュの未定乗数法に関しては今回は説明しませんので、違うサイトを参考にしてください。

この結果、最大の重みをもつ配置が得られます。

このときの配置はボルツマン分布として知られます。

以下に、ボルツマン分布の式をかきます。

$\huge \frac{N_i}{N}=\frac{e^{-βε_i}}{\sum\limits_{i}e^{-βε_i}}$​​

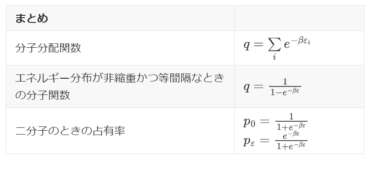
ボルツマン分布の分母$\sum\limits_{i}e^{-βε_{i}}$​を分配関数と言います。

分配関数

$q=\sum\limits_{i}e^{-βε_{i}}$​​

【参考】ラグランジュの未定乗数法を説明しているサイトや書籍

○ 高校数学の美しい物語 ラグランジュの未定乗数法と例題

https://manabitimes.jp/math/879

○ EMANの物理学 ラグランジュの未定乗数法

https://eman-physics.net/analytic/lag_method.html

○入門経済学のための微分・積分

○機械学習のエッセンス

https://amzn.to/2WkXVFG

https://amzn.to/3ycMQ7A