量子化学を学習する過程で必ずでてくる水素原子のシュレディンガー方程式。
1次元や2次元のシュレディンガー方程式とは違い複雑な形をしているためにつまずきやすいポイントでもあります。
水素原子のシュレディンガー方程式を解く流れとしては、
水素原子のハミルトニアンを極座標表示で表す→シュレディンガー方程式を書き表す→半径部分と角度部分に変数分離する→得られた二つの式を解く という風になっています。
今回はこの水素原子のシュレディンガー方程式の変数分離のところまでを考えていきましょう。
水素原子のシュレディンガー方程式
水素原子のシュレディンガー方程式は厳密に解けることが知られています。
逆に、水素原子以外、つまり電子が2つ以上になった途端に厳密にシュレディンガー方程式を解くことはできなくなります。
水素原子のシュレディンガー方程式を考えるに当たって、3次元のデカルト座標(x,y,z)で表すよりも、極座標(r,θ,φ)で表す方が都合がいいです。
そのため、水素原子のハミルトニアンとシュレディンガー方程式は極座標表示で書かれています。
具体的なシュレディンガー方程式
結論からいうと、水素原子のハミルトニアンは、
$$
\hat{H}=-\frac{\hbar^{2}}{2 m_{\mathrm{e}}} \nabla^{2}-\frac{e^{2}}{4 \pi \varepsilon_{0} r}
$$
のように表されます。
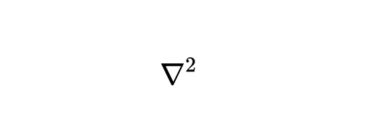
このとき\(\nabla^{2}\)はラプラス演算子と呼ばれるものです。
ラプラス演算子(ラプラシアン)についてはこちらの記事をご覧ください。
またハミルトニアン2項目の\(-\frac{e^{2}}{4 \pi \varepsilon_{0} r}\)に関しては水素原子核による電位(クーロンポテンシャル)を表しています。
そして、シュレディンガー方程式は、このハミルトニアンから計算すればよく
-\frac{\hbar^{2}}{2 m_{\mathrm{e}}}\left[\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial \psi}{\partial r}\right)\right.\left.+\frac{1}{r^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial \psi}{\partial \theta}\right)+\frac{1}{r^{2} \sin ^{2} \theta} \frac{\partial^{2} \psi}{\partial \phi^{2}}\right] \\
-\frac{e^{2}}{4 \pi \varepsilon_{0} r} \psi(r, \theta, \phi)=E \psi(r, \theta, \phi)
$$
水素原子のシュレディンガー方程式の変数分離
-\frac{\hbar^{2}}{2 m_{\mathrm{e}}}\left[\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial \psi}{\partial r}\right)\right.\left.+\frac{1}{r^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial \psi}{\partial \theta}\right)+\frac{1}{r^{2} \sin ^{2} \theta} \frac{\partial^{2} \psi}{\partial \phi^{2}}\right] \\
-\frac{e^{2}}{4 \pi \varepsilon_{0} r} \psi(r, \theta, \phi)=E \psi(r, \theta, \phi)
$$
\begin{aligned}
{-\hbar^{2}\left(\frac{\partial}{\partial r} r^{2} \frac{\partial \psi}{\partial r}\right)-\hbar^{2}\left[\frac{1}{\sin \theta}\left(\frac{\partial}{\partial \theta} \sin \theta \frac{\partial \psi}{\partial \theta}\right)+\frac{1}{\sin ^{2} \theta} \frac{\partial^{2} \psi}{\partial \phi^{2}}\right]}{-2 m_{\mathrm{e}} r^{2}\left[\frac{e^{2}}{4 \pi \varepsilon_{0} r}+E\right] \psi(r, \theta, \phi)=0}
\end{aligned}
$$
角度部分と動径部分
先ほど水素原子のシュレディンガー方程式が角度の部分(θ,φ)と半径の部分(r)で変数分離できることがわかりました。
ということは、波動関数も角度部分と半径の部分に分けられることを意味します。
そこで、つぎのように波動関数をおきます。
$$
\psi(r, \theta, \phi)=R(r) Y(\theta, \phi)
$$
このとき、R(r)の部分を動径波動関数、Y(θ,φ)を角波動関数ということがあります。
これを用いてシュレディンガー方程式を表し直します。先ほど求めたシュレディンガー方程式を変形したものに、\(\psi(r, \theta, \phi)=R(r) Y(\theta, \phi)\)を代入します。
そして代入したものを変数分離のために\(R(r) Y(\theta, \phi)\)で両辺を割ります。
そうすると完全に角度と半径で分けられることがわかります。
\begin{array}{c}
-\frac{\hbar^{2}}{R(r)}\left[\frac{\mathrm{d}}{\mathrm{d} r}\left(r^{2} \frac{\mathrm{d} R}{\mathrm{d} r}\right)+\frac{2 m_{\mathrm{e}} r^{2}}{\hbar^{2}}\left(\frac{e^{2}}{4 \pi \varepsilon_{0} r}+E\right) R(r)\right] \\
-\frac{\hbar^{2}}{Y(\theta, \phi)}\left[\frac{1}{\sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial Y}{\partial \theta}\right)+\frac{1}{\sin ^{2} \theta} \frac{\partial^{2} Y}{\partial \phi^{2}}\right]=0
\end{array}
$$
-\frac{\hbar^{2}}{R(r)}\left[\frac{\mathrm{d}}{\mathrm{d} r}\left(r^{2} \frac{\mathrm{d} R}{\mathrm{d} r}\right)+\frac{2 m_{\mathrm{e}} r^{2}}{\hbar^{2}}\left(\frac{e^{2}}{4 \pi \varepsilon_{0} r}+E\right) R(r)\right]=α
$$
-\frac{\hbar^{2}}{Y(\theta, \phi)}\left[\frac{1}{\sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial Y}{\partial \theta}\right)+\frac{1}{\sin ^{2} \theta} \frac{\partial^{2} Y}{\partial \phi^{2}}\right]=-α
$$
-\frac{1}{R(r)}\left[\frac{\mathrm{d}}{\mathrm{d} r}\left(r^{2} \frac{\mathrm{d} R}{\mathrm{d} r}\right)+\frac{2 m_{\mathrm{e}} r^{2}}{\hbar^{2}}\left(\frac{e^{2}}{4 \pi \varepsilon_{0} r}+E\right) R(r)\right]=β
$$
-\frac{1}{Y(\theta, \phi)}\left[\frac{1}{\sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial Y}{\partial \theta}\right)+\frac{1}{\sin ^{2} \theta} \frac{\partial^{2} Y}{\partial \phi^{2}}\right]=-β
$$
まとめ
今回のまとめです。
・水素原子のシュレディンガー方程式は厳密に解ける
・水素原子のシュレディンガー方程式は極座標を使って考える
・水素原子のシュレディンガー方程式は半径部分(r)と角度部分(θ,φ)を用いて変数分離できる
・変数分離して得られる二つの式は次のように表せる。
-\frac{1}{R(r)}\left[\frac{\mathrm{d}}{\mathrm{d} r}\left(r^{2} \frac{\mathrm{d} R}{\mathrm{d} r}\right)+\frac{2 m_{\mathrm{e}} r^{2}}{\hbar^{2}}\left(\frac{e^{2}}{4 \pi \varepsilon_{0} r}+E\right) R(r)\right]=β
$$
-\frac{1}{Y(\theta, \phi)}\left[\frac{1}{\sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial Y}{\partial \theta}\right)+\frac{1}{\sin ^{2} \theta} \frac{\partial^{2} Y}{\partial \phi^{2}}\right]=-β
$$
いかがだったでしょうか。このあとに次何を勉強するのか、それから量子化学を理解する上でのおすすめの参考書籍を紹介しています。そちらもぜひご一読してください。
つぎのステップ(波動関数を求める)
今回は水素原子のシュレディンガー方程式を動径部分と角度部分に分けるのをみていきました。
次のステップとしては、今回得られた二つの式をもとに波動関数を実際にもとめてみることになります。
そのとき、二つの式(半径の式と角度の式)を別々に解いていきます。
それはまた次回説明したいと思います。
おすすめの参考書籍
今回の内容は、マッカリーサイモン物理化学―分子論的アプローチ〈上〉 の6章とアトキンス物理化学(上)第10版のトッピック9Aでも同様のことが記述されていました。
どちらも東京化学同人から出版されておりとても信頼のできる書籍です。こちらの参考書を一読すれば、量子化学の大枠の部分は理解できるようになると思います。
もしも、このような教科書が理解できないという方には、もう少し基礎から量子化学、あるいはシュレディンガー方程式などを理解できる本を紹介します。
この参考書は、量子化学の基礎を入門者向けに詳しく説明しています。
白黒刷りなのが少し残念ですが、余白も多く見やすいレイアウトなので学習にそれほど支障はないでしょう。
数式でちゃんと説明しているため抽象的になりすぎず、根拠をもって理解することができます。
こちらはさらに初学者向けです。
数式をほとんど使わずに解説しています。
ただし、簡潔にまとめられている分、もう少し説明が欲しいと思う部分もいくつかありましたので、マッカリーサイモンの物理化学やアトキンス物理化学など詳しい教科書とともに読むのがいいでしょう。