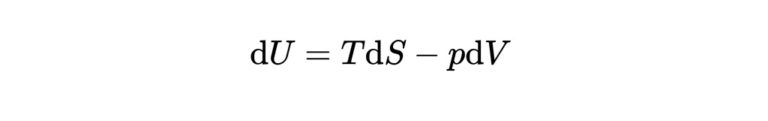これまで内部エネルギー、エンタルピー、ヘルムホルツエネルギー、ギブズエネルギーといった熱力学の状態量それぞれの意味をみていきましたが、今回はそれぞれを結びつけてできる式をみていきましょう。
これは熱力学の基本式といわれ、熱力学第一法則と熱力学第二法則を結びつけるのに非常に大切な式です。
熱力学の基本式
結論から言うと、ここで覚えるべき熱力学の基本式は4つです。
$$
\begin{aligned}
\begin{array}{l}
\mathrm{d} U&=&T \mathrm{d} S-p \mathrm{d} V\\
\mathrm{d} H&=&T \mathrm{d} S+V \mathrm{d} p \\
\mathrm{d} A&=&-p \mathrm{d} V-S \mathrm{d} T \\
\mathrm{d} G&=&V \mathrm{d} p-S \mathrm{d} T
\end{array}
\end{aligned}
$$
これらの関係式は各状態関数の微小変化と他の状態量との関係を表現したものです。
それぞれの導出は難しくないので、一度やってみると良いと思います。
ここでは、その中でも内部エネルギーの完全微分の式について導出してみます。
内部エネルギーの完全微分の導出
まず最初の式である\(\mathrm{d} U=T \mathrm{d} S-p \mathrm{d} V\)をみていきましょう。
そもそもこの式は、熱力学第一法則である\(\mathrm{d} U=T \mathrm{d} S-p \mathrm{d} V\)を用いて導き出せます。
可逆膨張の仕事は、
$$
\mathrm{d} w_{\mathrm{rev}} =-p\mathrm{d} V
$$
可逆の時におこった熱のやりとりは、エントロピーの定義より
$$
\mathrm{d} q_{\mathrm{rev}}=T \mathrm{d} S
$$
であるので、これを用いて\(\mathrm{d} U=T \mathrm{d} S-p \mathrm{d} V\)に代入すると、熱力学の基本式の一つ
$$
\mathrm{d} U=T \mathrm{d} S-p \mathrm{d} V
$$
が求められます。
dUは完全微分ですので経路に依存せず、可逆条件のもとで得られたこの式を非可逆的に行われたとしても同じ値が求められるようになります。
内部エネルギーの基本式の意味
上のように求められた内部エネルギーの基本式ですが、この式の性質をみていきましょう。
$$
\mathrm{d} U=T \mathrm{d} S-p \mathrm{d} V
$$
まず、この式は内部エネルギーが変化をエントロピーSと体積Vが担っていることを意味します。
もちろん、他の圧力や温度といった指標で表すことも可能ですが、式のシンプルさからこの二つ(S,V)が変数であると考えたほうが都合がよいことになります。
そもそも数学の全微分の式から
$$
\mathrm{d} U=\left(\frac{\partial U}{\partial S}\right)_{V} \mathrm{d} S+\left(\frac{\partial U}{\partial V}\right)_{S} \mathrm{d} V
$$
ですので、前の式と比べて
$$
\left(\frac{\partial U}{\partial S}\right)_{V}=T \quad\left(\frac{\partial U}{\partial V}\right)_{S}=-p
$$
という二つの式が求められます。
一つ目の式は、体積一定のもとエントロピーと内部エネルギーの比が絶対温度になることを意味し、二つ目の式は、一定エントロピーのもと、体積と内部エネルギーの比は、圧力の符号を逆にしたものに等しいということを意味します。
このように熱力学の基本式は、それぞれの状態量の間の関係性を示すものになります。
感覚的に理解できるものもあれば、予測できなかった式が導かれることもありますので、じっくり観察してみましょう。
発展:マクスウェルの関係式
熱力学の基本式の関係は上に述べたように求められることがわかりましたが、ここからさらに発展した形で表現することができます。
結論から言うと、それはマクスウェルの関係式と呼ばれます。
それではその式の導出についてみていきましょう。
マクスウェルの関係式
数学において、ある関数\(f(x, y)\)の無限小の変化は、\(\mathrm{d} f=g \mathrm{d} x+h \mathrm{d} y\)と表されます。
このとき、dfが完全微分ならば次の式が成り立ちます。
$$
\left(\frac{\partial g}{\partial y}\right)_{x}=\left(\frac{\partial h}{\partial x}\right)_{y}
$$
このことから、内部エネルギーに関する熱力学の基本式\(\mathrm{d} U=T \mathrm{d} S-p \mathrm{d} V\)に関してもこの式が成立するので、
$$
\left(\frac{\partial T}{\partial V}\right)_{S}=-\left(\frac{\partial p}{\partial S}\right)_{V}
$$
というマクスウェルの関係式が得られます。
このマクスウェルの式も、状態量の間の関係を示すものです。今回は内部エネルギーの式から求めましたが、エンタルピー、ヘルムホルツエネルギー、ギブズエネルギーのそれぞれにおいて同様のことが考えられるので、他に3つのマクスウェルの関係式が求められます。
まとめ
今回の熱力学の基本式とマクスウェルの関係式は次の表のようにまとめられます。
| 状態関数(U,H,A,G) | 熱力学基本式(完全微分の形) | マクスウェル関係式 |
| U | $$ \mathrm{d} U=T \mathrm{d} S-p \mathrm{d} V $$ |
$$ \left(\frac{\partial T}{\partial V}\right)_{S}=-\left(\frac{\partial p}{\partial S}\right)_{V} $$ |
| H | $$ \mathrm{d} H=T \mathrm{d} S+V \mathrm{d} p $$ |
$$ \left(\frac{\partial T}{\partial p}\right)_{S}=\left(\frac{\partial V}{\partial S}\right)_{p} $$ |
| A | $$ \mathrm{d} A=-p \mathrm{d} V-\mathrm{SdT} $$ |
$$ \left(\frac{\partial p}{\partial T}\right)_{V}=\left(\frac{\partial S}{\partial V}\right)_{T} $$ |
| G | $$ \mathrm{d} G=V \mathrm{d} p-S \mathrm{d} T $$ |
$$ \left(\frac{\partial V}{\partial T}\right)_{p}=-\left(\frac{\partial S}{\partial p}\right)_{T} $$ |
マクスウェルの関係式などは覚えなくてもいいですが、熱力学の基本式から瞬時に思い浮かべることができるようにしておきましょう。